Interview No.37　鈴木 龍正
理学院

　

東京工業大学理学院数学系数学コースの鈴木龍正です。
休日はパズル雑誌の問題を解いて過ごしています。
東工大の好きなところは数学に限定しても多種多様な最先端の研究を行っている方々が身近にいるところです。

研究概要 / Research Outline

　私は数学の一分野である位相幾何学の研究をしています。特に、4次元多様体の微分構造について、Gluck手術の一般化でトーラス手術の特別な場合に相当する、ポシェット手術を研究しています。Gluck手術とトーラス手術は、どちらも互いに同相であるが微分同相ではないエキゾチックな4次元多様体の組を構成する手法です。トーラス手術の具体的な構成法をハンドル図式と呼ばれる、微分構造を特定する際に有効な図式で見ることは、多くの場合非常に困難です。しかし、ポシェット手術は手術後のハンドル図式を入手しやすいことが利点です。
　また、3次元多様体は手術図式と呼ばれる図式で微分構造を表現できます。手術図式はその3次元多様体を境界に持つ4次元多様体の図式と明確に対応付け可能であることから、3次元多様体がどの4次元多様体の境界になり得るかを調べることは、4次元多様体の微分構造を理解するために有効です。3次元多様体の最も基本的かつ重要なクラスの一つに3次元Brieskornホモロジー球面がありますが、それを境界に持つ4次元多様体が何かはまだほとんど理解されていませんので、この問題の解明に向けても研究を行っています。

私の最初の単著論文に現れる4次元の図式の変形過程について

　私の最初の単著論文「Constructions of homotopy 4-spheres by pochette surgeries」の9-10ページ目には、枠係数と呼ばれる係数が<0>の2個の閉曲線の間にある非自明で複雑な閉曲線が描かれた図が記載されています。これは、ポシェット手術後に得られる4次元多様体の微分構造を表すハンドル図式を書くための設計図の役割を果たしています。4次元多様体のハンドル図式(Kirby図式とも呼ばれています)を長年取り扱う専門家の方には、この図式とスライドの手順を見ることで理解できますが、このような独特の変形操作になじみがない方には理解しにくいのではないかと思いました。博士課程在学時に、この図の変改過程に関する質問等が数学の専門家、非専門家の両方から寄せられましたので、この複雑な閉曲線を描くための具体的な手順をここで紹介したいと思います。

　今回は係数<0>の閉曲線の一方に2回、もう一方に3回絡まる場合に限定して紹介したいと思います。このように絡まり方を固定すると、微分構造を考える際には4通りに絞られます(他の絡まり方で固定しても同様に4通りに絞られます)。他の絡まり方の場合も工程数が増えて曲線が複雑になるだけで本質的に同じ変形操作を繰り返すことで一般の場合に対する私の最初の単著論文の9-10ページ目にある図が得られます。

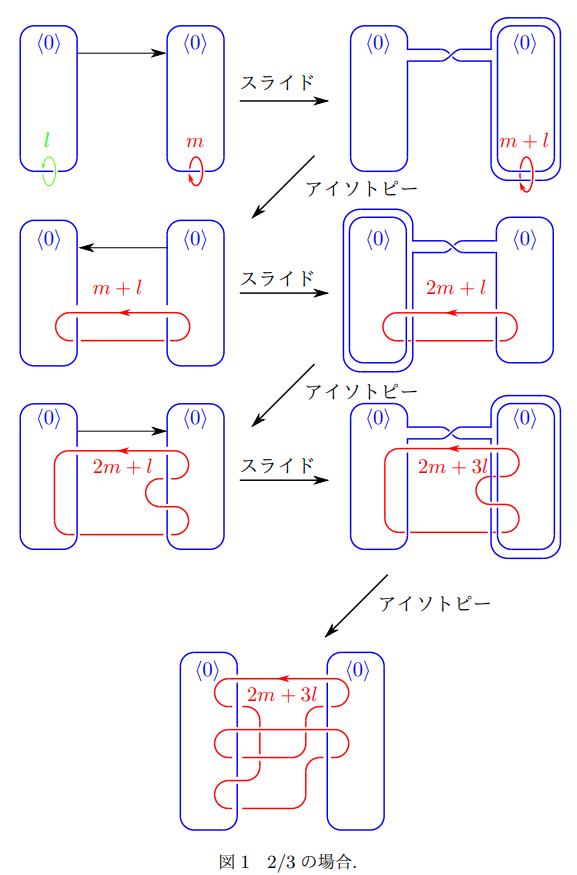
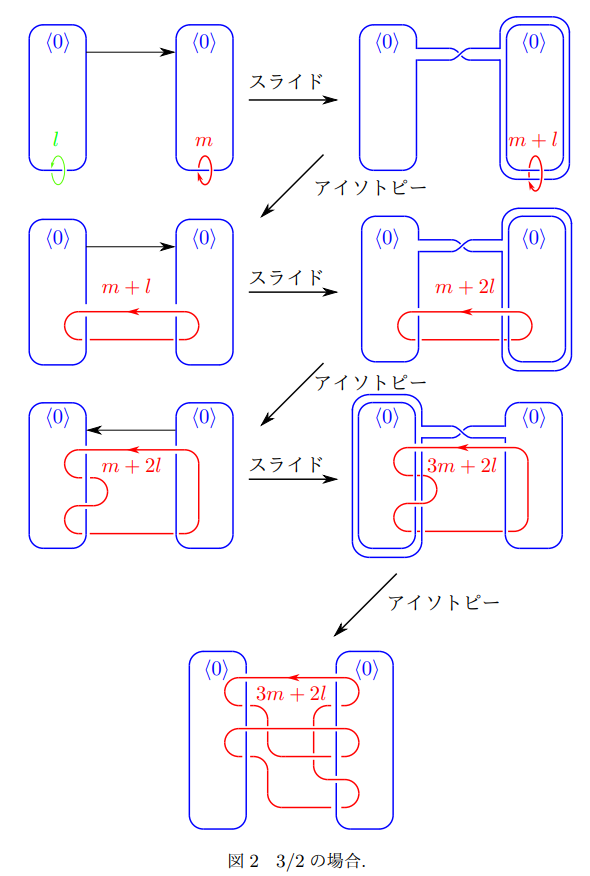
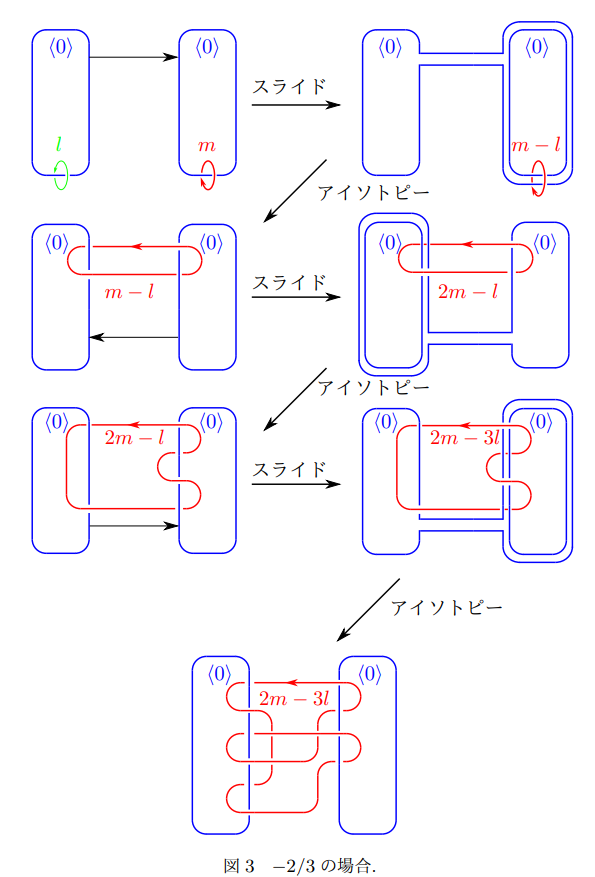
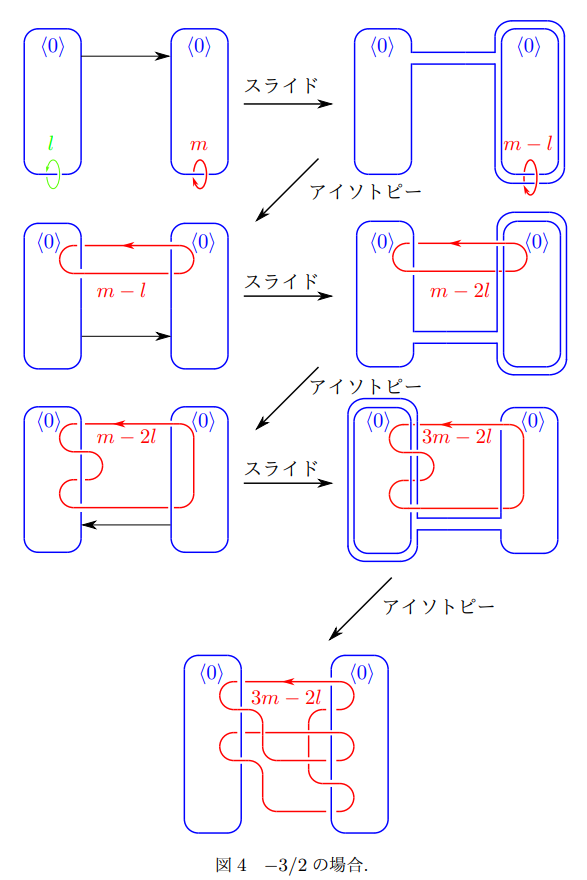
　図1-4に記載されているスライドとアイソトピーの操作は共に微分構造を変えない変形になります。スライドと書かれている変形過程は、3次元閉多様体の手術図式や4次元多様体の(相対)ハンドル図式特有の変形過程になりますが、操作の仕方が帯の付け方以外は、2個の青い閉曲線の傍に書かれている数の情報を基に一通りに決まります。一方、アイソトピーと書かれている変形過程は、慣れていないと変化の過程を追うことが難しいこともありますが、ビニール紐や毛糸で実際にこれらの絡まり方を再現した模型を作り動かすことで同様に変化の過程を追うことが可能な変形法になります。

　ポシェット手術後に得られる4次元多様体の微分構造は図中にあるmとlの係数から定まる分数で定まることが知られています。今回限定した場合は2/3, 3/2, -2/3, -3/2に相当し、それぞれ図1, 2, 3, 4の場合に相当します。図1は以前私と同じ遠藤 久顕研究室に在籍されていた方の修士論文で考案された変形過程になります。図2は図1から容易に得られましたが、図3, 4は図1, 2の上の方で帯をとるスライドではなく、下の方から帯をとるスライドを行うことで、図1, 2と同様の規則性が比較的わかりやすい閉曲線が得られることに気づく必要がありました。

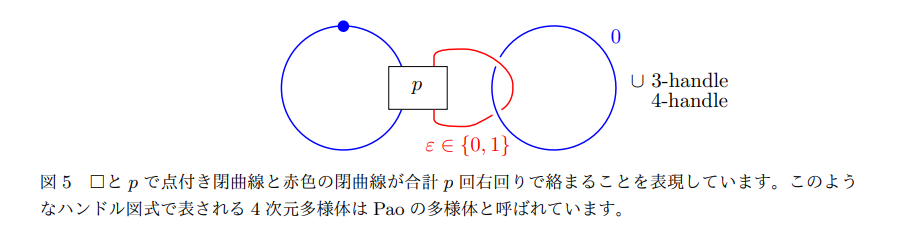
　図1-4と私の最初の単著論文の8ページ目の変形過程を用いることで、4次元閉多様体の中でも最も基本的な例である4次元球面上のある特別な場合のポシェット手術の微分構造を図5のように描くことで特定することができます。

メッセージ / Message

　現代の数学、特に位相幾何学の研究の具体的な過程は、他分野の方が良く知るための機会があまりないのではないかと思います。今回取り扱った話題は研究内容のほんの一部でしたが、少しでも多くの方に位相幾何学と4次元多様体を研究する際に用いられる独特の魅力的な研究手法に興味を持っていただけたらと思い、今回の題材をこの場で書かせて頂きました。更に今後の研究等の知的創造及び探究活動に役立てていただけたら幸いです。